Monetary policy models: lessons from the Eurozone crisis

The model

Within the philosophy of the limited participation models in Fuerst (1992) and Christiano and Eichenbaum (1992), the present model extends the structure and ideas in Gutiérrez (2006) and Gutiérrez and Palmero (2013). As explained above, limited participation models have already satisfactorily answered some of the questions under analysis without detracting from the framework of a competitive economy, a reasonable assumption for the Eurozone. On this basis, we assign a central role to the ratio of total loans to total deposits in the economy’s financial sector. The reasons are manifold. On the one hand, in a general equilibrium economy where the monetary policy operates through a financial intermediary, the leverage ratio is a natural candidate to explain how the bank lending channel operates. On the other hand, this ratio captures the reduction of the loans issued by financial institutions, which later causes declines in aggregate investment and demand. Finally, the leverage ratio allows the relevant linkages between the transmission mechanism, financial ratios, and balance sheets to be consistently integrated, an important question in the literature widely analyzed, among others by den Haan et al. (2007), Adrian and Shin (2008), Schularick and Taylor (2012), Claessens et al. (2012), Gambetti and Musso (2017), Bonci and Columba (2008), and Keister and McAndrews (2009). Indeed, since financial sector loans are debts of firms, this ratio reflects both the balance sheets of banks and firms. As we show in this section, we can interpret the leverage ratio as the fixed-assets-to-total-assets ratio of households, a measure of the financial leverage degree of households, who are the ultimate owners of the economy. For this reason, loan-to-deposit ratio, financial leverage, and leverage ratio are terms used interchangeably in the rest of the paper.

More specifically, and for our purposes, this loans-to-deposits leverage ratio allows us to make two prominent extensions in the model. The first is the detailed microeconomic incorporation of the financial decisions of households and firms, and the subsequent specifications of both the intermediation role played by banks and the way the economy is affected by ECB instruments. Within this context, this ratio details and disentangles the underlying links between inflation, monetary policy instruments, and transmission channels. The second extension arises from the endogenous nature of inflation, interest rates, and the volume of bank loans. In our model, these variables become linked by long-run steady relationships where simultaneous increases in money supply, decreases in real interest rates, deflation, and aggregate demand descents are possible, offering an explanation of the observed debt–deflation mechanisms.

The theoretical description of the economy is simple. There are four agents in the economy: households, financial intermediaries, firms, and a central bank. Households employ their wealth to consume and save. Firms provide final goods to the households, obtaining labor services from the households and capital services from the financial intermediaries. Financial intermediaries channel funds from households to production firms and own all capital in the economy. This is a reasonable approximation since, in the EU, bank loans traditionally finance most investments. The central bank compels the financial intermediaries to hold a percentage of the households’ deposits as reserves and carries out the monetary policy by controlling interest rates and money supply. In this respect, it is assumed that the financial sector is the intermediary means by which the monetary policy is conducted. Finally, markets are competitive.

Money is introduced in the sense of Clower (1967). Following Lucas (1980, 1982), trading is divided into different sessions. In the first session, immediately before each period t, labor and asset markets for the period t open and close. Subsequently and immediately after each period t, each household receives the payment for the previous period’s labor services from the production sector. Households also receive the savings accumulated during the previous period plus their returns from the financial intermediaries. The central bank takes monetary policy measures, and households and firms carry out buying and selling activities for consumption and capital goods. As in Lucas (1990), it is assumed that households purchase goods and financial assets using their initial money balances.

Households’ behavior can be described through a representative consumer. In particular, the per-capita demands for consumption goods, assets, and money, and the labor and capital supplies, are given by the following problem:

where \(\beta ,t,{{{\mathcal{U}}}},{C}_{t},\overline{h}\), and \({l}_{t}^{\rm {{S}}}\) are, respectively, the time discount factor, the period of time, the Bernoulli utility function, the consumption at period t, the time endowment, and the labor supply at period t. The first constraint represents the cash-in-advance constraint that applies in the goods and assets markets at period t, where \({p}_{t},{C}_{t},{D}_{t+1}^{\rm {{S}}}\), and \({M}_{t}^{\rm {{D}}}\) are, respectively, the price of the consumption good at period t, the consumption of goods at period t, the amount of money devoted to buying assets at the end of period t—i.e., the supply of deposits—and the holding of money at the beginning of period t—i.e., the demand of money. The timing of decisions relevant to the correct interpretation of how money demand is formulated is the following. At each period t, households use the money obtained at the beginning of the period to buy along this entire period consumption goods (C_t) and decide at the end of the period and once they have determined consumption how much money to devote for bank deposits (D^S), which therefore measures the amount of money saved over the period. This supply of bank deposits at period t is also a demand/purchase of assets against the financial intermediaries, yielding interest in the following period t + 1. This variable D is, by its nature, a variable playing a double role as a source of expenditure in one period and of income in the following, therefore appearing in the budget constraints of both periods t and t + 1. The assigned time index must be unique, and by convention in monetary general equilibrium models such as ours, the time index refers to the period at which the asset is a source of wealth t + 1 (see, for instance, Gutiérrez, 2006; Heer and Maussner, 2005; Hodrick et al. 1991, or Ljungqvist and Sargent, 2018). Accordingly, in our cash-in-advance in everything model, \({D}_{t+1}^{{\rm {S}}}\) must be understood as the amount of money that at period t is used by households to buy assets/deposits, that is, as a component of the demand of money at period t. To clarify the double dimension of D_t+1 as a demand/purchase of assets and a supply/offer of deposits, we incorporate the superscript S.

The second constraint states that the holding of money at period t + 1 is given by the labor and deposits remunerations plus the amount of money unspent at period t. As usual, w_t and i_t denote the real wage and the nominal interest paid to deposits. The third constraint captures the non-existence of the money illusion: in order to accept exchanges based on money and the described timing scheme, each household requires that, in the whole time horizon, the total discounted nominal value of its consumption should not be lower than the total discounted nominal value of their wealth.

In the first session of period t, the financial sector demands (through the sale of assets) the amount \({D}_{t}^{\rm {{D}}}\) of deposits from the households, and the central bank takes the monetary policy measures fixing the legal reserves coefficient s_t, the money supply change G_t, and implementing the control of interest rates. To simplify notation, we anticipate that, at the financial equilibrium, \({D}_{t}^{\rm {{S}}}={D}_{t}^{\rm {{D}}}={D}_{t}\). As a consequence, the financial sector keeps s_tD_t as reserves in the central bank, so this amount is unavailable for productive capital—i.e., production firms cannot borrow it—but, at the same time, the money supply changes G_t is added to the quantity of resources available for supplying productive capital—i.e., the amount that production firms can borrow. Therefore, the financial sector can supply productive capital up to a value (1−s_t)D_t + ρ_tG_t, where ρ_t is the percentage of the money supply change which becomes productive capital and accumulates the difference for the next period. Since this accumulated fraction of the deposits constitutes a resource accumulated during period t−1 for the (next) period t, and it aims to eliminate bankruptcy risks, it will be considered as a demand for financial capital goods. At the first session of period t, denoting the per-capita household’s deposits in real terms^{Footnote 5} by \({d}_{t},{d}_{t}=\frac{{D}_{t}}{{p}_{t-1}}\), the productive capital by \({K}_{t}^{\rm {{P}}}\), and the financial capital by \({K}_{t}^{\rm {{F}}}\), and assuming that the central bank formulates the increases in the money supply G_t as a percentage g_t of the amount of deposits D_t –i.e., G_t = g_tD_t–, then

At period t, the financial sector owns all the capital factors in the economy \({K}_{t}^{\rm {{P}}}+{K}_{t}^{\rm {{F}}}\), provides capital services to the production firms, and must return the deposits plus their interest to the households. Strictly speaking, the financial sector decides the supply of productive capital, that is, the quantity of productive capital to be lent to the production sector, and the production sector decides the demand for productive capital, i.e., the amount of capital to be borrowed from the financial sector, and therefore also the demand of financial capital. In equilibrium, demand equals supply, and to simplify notation, we consider \({K}_{t}^{\rm {{P}}}\) as both demand and supply of productive capital. Then, in per-capita terms, the problem solved by this financial sector is

where Π_t are the financial sector profits, \({r}_{t}^{\rm {{P}}}\) is the rental price of capital paid by production firms to financial firms, and δ is the depreciation rate, defined on the total capital^{Footnote 6}\(({K}_{t}^{\rm {{P}}}+{K}_{t}^{\rm {{F}}})\). The consideration of the market structure of the financial sector is in our model of particular interest. On the one hand, the market structure is an important causal factor of the sector profits. On the other, due to the trade-offs between competition and financial stability, it implies an optimum that must be carefully determined by the policymakers, especially in periods of crisis such as the GFC here considered: Effective competition translates into lower bank’s interest margins and higher social welfare, but it can also imply higher financial fragility and instability leading to bankruptcies, also prejudicial in terms of social welfare (see for instance Allen and Gale, 2004; Benchimol and Bozou, 2022; Jiménez et al., 2010). In addition and as the empirical analysis by Kim (2018) concludes, this trade-off seems to be dependent on the bank size, being particularly present for small banks. In this respect, the battery of measures implemented by the ECB and the European Commission promoting controlled and supervised bank mergers and safeguarding internal competition (see Koopman, 2011), appears as the most effective policy to ensure both financial stability and social welfare. We refer the interested reader to Benchimol and Bozou (2022), where these questions are theoretically and quantitatively analyzed. Regarding the market structure of the Eurozone financial sector, the empirical analyses of the usual market power indexes suggest that, as a result of the continuous and deep harmonizing and macroprudential policies, the financial sector structure is oligopolistic but not too far from perfect competition (see Căpraru et al. 2020; Cruz-García et al. 2017). Assuming that markets are competitive, the number of financial intermediaries adjusts until the condition of zero profits is verified, and then

where \({p}_{t-1}{K}_{t}^{\rm {{P}}}=(1-{s}_{t}+\rho {g}_{t}){D}_{t}\) and \({p}_{t-1}{K}_{t}^{\rm {{F}}}={D}_{t}-{p}_{t-1}{K}_{t}^{\rm {{P}}}\), since the first constraint in problem (2) always binds if prices are positive. As shown in Appendix A of the supplementary section, if we define the real interest rate paid by financial intermediaries to household deposits by \({r}_{t}^{\rm {{H}}}-\delta\), this zero profits condition can also take the form of

This zero profits equilibrium condition deserves a deeper examination. First, as shown in Appendix A, it implies that the interest rate charged by banks to firms, \({r}_{t}^{\rm {{P}}}\), must necessarily be higher than the interest rate banks pay to deposits, \({r}_{t}^{\rm {{H}}}-\delta\). In this respect, it is worth noting that, in standard monetary general equilibrium models including a financial sector, this interest rate spread emerges either as a mark-up stemming from the monopolistic competition financial market structure, as in Bernanke and Gertler (1995), or because of the consideration of a non-zero private sector’s default probability, as in Corsetti et al. (2013). In our model, since the official reserves requirement aims to remove default risks, the interest rate spread is a natural consequence of the competitive economy that internalizes financial risk and implements the above-quoted instrument to remove the risk of bank default. Jointly with this interesting theoretical result, condition (4) clarifies the role played by the ECB standing facilities. As is well known, the ECB controls interest rates, mainly by fixing the rates on the deposit facility and the marginal lending facility^{Footnote 7}. The deposit rate establishes the floor on the market interest rate for bank loans since no bank will lend money out at less than what it can earn at the deposit facility in the ECB. The lending rate constitutes the ceiling on the market interest rates, given that this rate is the cost at which any bank can obtain liquidity from the ECB. Using these standing facilities, the ECB controls the money market interest rates within a corridor, whose range, denoted by Q_t, plays a crucial role. First, concerning the interest rate paid to the household’s deposits, \({r}_{t}^{\rm {{H}}}-\delta\), and the interest rate perceived by the financial sector, \({r}_{t}^{\rm {{P}}}\), the control of interest rates by the central bank in our competitive economy results in a margin for \({r}_{t}^{\rm {{H}}}\) concerning \({r}_{t}^{\rm {{P}}}\) given by \({r}_{t}^{\rm {{P}}}-{r}_{t}^{\rm {{H}}}={Q}_{t}+\delta ={m}_{t}\). Second, this margin also has consequences for the variable ρ, the percentage of the money supply change that becomes productive capital. Indeed, although the variable ρ is not included in condition (3), its value is determined by the (equivalent) zero profits condition (4):

In economic terms, once the central bank decides s_t and g_t and fixes the differential m_t between perceived and paid interest rates, the zero profits condition determines ρ_t. As explained before, ρ is the percentage of the money supply change lent to the production firms. Therefore, it is logical to find that ρ_t depends on the number of financial firms, which in turn is a consequence of the verification of the zero profits condition, which, at the same time, depends on each established margin m_t. This implies that ρ_t is an endogenous variable whose equilibrium value is jointly determined with the model’s remaining endogenous variables. We clarify these aspects in Appendix A of the supplementary information.

Production is given by the function \({y}_{t}=F({K}_{t}^{\rm {{P}}},{l}_{t})={({K}_{t}^{\rm {{P}}})}^{\alpha }{l}_{t}^{1-\alpha }\). This function governs the production of the unique good of the economy, which can be used as a consumption good C_t, productive capital good \({K}_{t+1}^{\rm {{P}}}\) (that allows the productive activity of firms), or financial capital good \({K}_{t+1}^{\rm {{F}}}\) (that allows bankruptcy risk to be removed). Given our assumptions, the problem solved by the production sector is, in per-capita terms:

where we have already considered that, at equilibrium, the demand for productive capital of the production sector equals the supply provided by the financial sector.

Regarding the money market, and since all constraints in the household’s problem become binding (see Appendix A of the supplementary information), the money demand at period \(t,{M}_{t}^{\rm {{D}}}\), is given by the expression \({M}_{t}^{\rm {{D}}}={p}_{t}{C}_{t}+{D}_{t+1}\). As explained before, the demand for money is composed of the amount of money used to buy consumption goods along the period, p_tC_t, plus the amount of money saved that period and devoted to making bank deposits, D_t+1. Given the intertemporal nature of this saving variable, the time index assigned by convention is the period at which they yield returns, period t + 1. However, since this is the amount of money demanded to make bank deposits at period t, the price level to be considered in order to formulate this demand of money in real terms is p_t:

The money supply, \({M}_{t}^{\rm {{S}}}\), fixed by the central bank but also determined by the financial sector, is given by \({M}_{t}^{\rm {{S}}}={\rho }_{0}{M}_{0}+\mathop{\sum }\nolimits_{j = 0}^{t}{\rho }_{t}{G}_{t}\), where M₀ and G_t are decided by the Central Bank. The money market clearing condition is therefore

We can now define the competitive general equilibrium for this economy. As usual, this equilibrium is defined as the sequences of prices and decisions such that: each agent solves its problem, taking as given the variables out of its control; profits are zero; and markets clear. The formulation of this equilibrium is somewhat burdensome. However, we can simplify by following the line of reasoning presented in Cooley and Prescott (1995) and Heer and Maussner (2005) and applied by Gutiérrez (2006) and Gutiérrez and Palmero (2013) in a parallel limited participation model. Indeed, as shown in detail in Appendix A of the supplementary material, it is possible to formulate the equilibrium in real terms as the solution to the following equivalent Social Planner’s Problem:

Definition 1

(Equivalent social planner’s problem formulation) In real terms, the equilibrium of the Economy is given by the sequences \({\{{\hat{\gamma }}_{t}\}}_{t = 0}^{\infty },{\{{\hat{C}}_{t}\}}_{t = 0}^{\infty },{\{{\hat{l}}_{t}\}}_{t = 0}^{\infty }\) and \({\{{\hat{d}}_{t}\}}_{t = 0}^{\infty }\) such that:

• Given \({\{{\hat{\gamma }}_{t}\}}_{t = 0}^{\infty }\), the sequences \({\{{\hat{\rho }}_{t}\}}_{t = 0}^{\infty },{\{{\hat{C}}_{t}\}}_{t = 0}^{\infty }\), \({\{{\hat{l}}_{t}\}}_{t = 0}^{\infty }\) and \({\{{\hat{d}}_{t}\}}_{t = 0}^{\infty }\) solve the Social Planner’s problem

  $$\begin{array}{c}\mathop{\max }\limits_{{C}_{t},{l}_{t},{d}_{t+1}}\mathop{\sum }\limits_{t=0}^{\infty }{\beta }^{t}{{{\mathcal{U}}}}({C}_{t})\\ {\rm {s.t.}}\qquad {C}_{t}+{d}_{t+1}\le {[{\hat{\gamma }}_{t}{d}_{t}]}^{\alpha }{({l}_{t})}^{1-\alpha }+{d}_{t}(1-\delta ),\\ 0\le {l}_{t}\le \overline{h},\\ {C}_{t},{d}_{t+1}\ge 0,\\ t=0,1,\ldots ,\infty ,\qquad {d}_{0}\,\,{{\mbox{historically given}}}\,.\end{array}$$

  (6)

• The sequence \({\{{\hat{\gamma }}_{t}\}}_{t = 0}^{\infty }\) verifies

  $${\hat{\gamma }}_{t}=1-\frac{{m}_{t}}{\alpha {({\hat{\gamma }}_{t}{\hat{d}}_{t})}^{\alpha -1}}\quad \forall t.$$

  (7)

We thus count on a simple formulation to study the monetary general equilibrium as well as the real and nominal effects caused by monetary policies and changes in the leveraging policy of firms. The sequences \({\{{\hat{C}}_{t}\}}_{t = 0}^{\infty },{\{{\hat{l}}_{t}\}}_{t = 0}^{\infty }\) and \({\{{\hat{d}}_{t}\}}_{t = 0}^{\infty }\) provided by the social planner’s problem coincide with those in the monetary general equilibrium. Regarding all the other variables in the monetary general equilibrium, and as explained in Appendix A of the supplementary information, they can be obtained from the equivalent social planner’s problem by applying the following relationships:

The role of the loan-to-deposit ratio

This social planner’s problem formulation constitutes an operative and manageable framework to study the monetary general equilibrium. For our purposes, one of its virtues is the incorporation of the loan-to-deposit ratio as a key variable in explaining the economic dynamics. From the mathematical point of view, this is done through the introduction of the social planner’s problem formulation of a new variable, γ. As we show in Appendix A of the supplementary section, this new variable, defined as

has an immediate interpretation in monetary, financial, and economic terms, being equivalent to the loan-to-deposit ratio of the financial sector. Since

and we are assuming that firms acquire all their productive capital by borrowing it from financial intermediaries, the total amount of loans in our economy coincides with the productive capital \({K}_{t}^{\rm {{P}}}\), and therefore

Therefore, decreases in γ_t respond to relative descents in productive capital, financial sector loans, and productive firms’ total debt, all ultimately constituting a financial deleveraging process. Given that financial leverage is defined as the use of borrowed money to obtain production and profits, and since all productive capital is financed by bank loans, lower values of γ_t imply the presence of a financial deleveraging process for the whole economy. Alternatively, as \({K}_{t}^{\rm {{P}}}\) takes the form of physical capital, γ_t is the fixed-assets-to-total-assets ratio from the position of households, that is, their operating leverage. In our general equilibrium model, households are the ultimate owners of the economy, so business risk and financial risk coincide (see, for instance, Brealey et al., 2014), and γ can be understood both as the operating and the financial leverage degree of the economy as a whole. For interpretations and analyses of this and similar financial leverage ratios, we refer the interested reader to ECB European Central Bank (2012), Schularick and Taylor (2012), or Mendoza and Terrones (2014).

Through this new variable γ_t, we can consider and study not only the consequences of monetary policies changing the reserves coefficient s_t and the money supply g_t, but also the effects of modifications in structural characteristics idiosyncratic to the financial intermediary sector, captured by the parameter ρ_t. Our proposal, therefore, constitutes an interesting option to analyze and theoretically explain the observed links between credit, monetary policy, inflation/deflation, debt, leverage, financial cycles, and real cycles identified by the empirical literature mentioned in this manuscript. Indeed, as shown in the following subsection, this total loans-to-total deposits ratio γ_t appears as the key variable in the monetary transmission mechanism, governing the real and nominal effects of the ECB policy measures on all the variables in the economy.

Loan-to-deposit ratio, transmission mechanism, and debt–deflation process

Let us now consider one of our central hypotheses, namely the existence of stable inflation targeting for the ECB and then of long-run relationships between the variables controlled by the ECB and involved in the transmission mechanism, and inflation. If we solve the social planner’s problem (6), we reach the following first-order necessary and sufficient conditions:

Since this model represents the detrended dynamics, let us look for a long-run steady-state in which the margin m_t charged by the financial sector, the legal reserves coefficient s_t, and the changes in money supply expressed as a percentage of nominal deposits g_t, are constant. Let these steady-state values be m, s, and g. As we prove below, this steady state exists, and all the variables remain constant with the only exception of prices p_t and the money supply increases G_t.

To see this, let us consider condition (7) of the social planner’s problem formulation. In the steady state, the deposits in real terms must be constant, and as m_t and d_t are constant, so is γ_t. Then, from the first order necessary condition, at this steady-state

From this expression, we obtain that the per-capita deposits in real terms d positively depend on the parameter γ. Analogously, from the second first-order condition, the steady-state value for the per-capita consumption is given by

which, we can show after some algebra, positively depends on the parameter γ.

In this detrended steady state, the aggregate per-capita capital stock is constant and given by

Denoting with I the detrended per-capita real investment, by definition that replacing depreciation, we arrive at I = δK^P = δγd, which also positively depends on the parameter γ.

In our model and as shown in Appendix A of the supplementary information, \({\hat{l}}_{t}=\overline{h}\). Taking \(\overline{h}=1\),

and therefore the steady-state values of the rental price of capital r^P and of the real wage w are

This implies that the real interest rate r^P negatively depends on the ratio γ, this dependence being positive for the real wage.

Regarding ρ and according to its definition, its steady-state value is

which positively depends on the loan-to-deposit ratio γ. Let us now study inflation in this model, denoted by π_t. Since the price level is given by

we get that, at the steady-state where \({\rho }_{t},\hat{{C}_{t}}\) and \(\hat{{d}_{t}}\) are constant,

Therefore, at the assumed steady-state,

a result consistent with empirical results and theoretical analyses. In our steady-state \({G}_{t}={g}_{t}{\hat{d}}_{t}{\hat{p}}_{t-1}=gd{\hat{p}}_{t-1}\), and from the former equation we obtain

According to our expression for \({\hat{p}}_{t-1}\), at the steady-state

and, consequently, the inflation rate at the steady state is also constant and given by

Summing up, we have shown that if the central bank fixes a constant legal reserves coefficient s, a constant percentage of nominal deposits g to formulate the money supply changes and a constant margin m to establish the interest rate paid to household deposits, then there exists a steady-state implying constant values for all variables in the monetary general equilibrium except for prices p_t and the money supply increases G_t. In addition, there exists a constant steady-state value for inflation, which is endogenously determined and that, as with the values of all the other endogenous variables, depends on the loan-to-deposit ratio of the financial sector.

The dependence of all these steady-state values on γ can also be analyzed after substituting d for its steady-state expression. Since we are specifically interested in the hypothesized existence of long-run steady links between the variables in the interest rate channel, bank lending channel, and inflation, we focus on the expressions for the interest rate and inflation. After substituting d for its steady-state expression, we obtain

which implies a negative relationship between the real interest rate and the loan-to-deposit ratio, and

which indicates a positive relation of inflation π to γ. Thus, from our steady-state expressions, we conclude that in the long run, there exist two equations linking these three variables, a finding consistent with the inflation objective of the ECB and the presence of an interest channel and a bank lending channel as transmission mechanisms, and justifying the implementation of a VEC model to analyze the empirical data consistently.

On this point, it is worth noting two questions. First, from Eqs. (8) and (9), the influence of interest rates and bank loans on prices, the so-called interest channel and bank lending channel, are exerted through the leverage ratio γ. Indeed, this variable γ enters as a fundamental in all the functions explaining the steady-state values. Since this ratio γ is given by the expressions

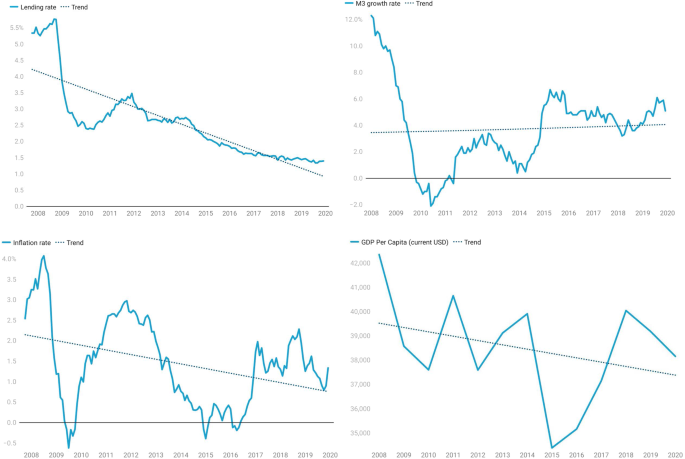
that depend on the reserves coefficient s_t, the range m_t of the corridor established by the standing facilities, and the money supply changes g_t, the variable γ_t is ultimately responsible for the monetary transmission mechanism. Second, these long-run relationships in Eqs. (8) and (9) also agree with the presence of debt–deflation processes observed by several researchers in the Eurozone during the crisis. For our purposes and as commented on in the first section, it is interesting to remark that the debt–deflation theory implies a negative relationship between the real interest rate and the loan-to-deposit ratio, a positive dependence of inflation on γ, and a negative relationship between inflation and the real interest rate, such as those identified by our long-run theoretical expressions linking π, γ and r^P. Therefore, expressions (8) and (9) summarize the links between debt–deflation channels, monetary policy instruments, and financial leverage depicted in Fig. 2.

It is worth noting the consistency of our model with the mechanisms and effects constituting the empirical and theoretical foundations of monetary theory. In particular, if we consider a temporary increase in money supply, the above equations describing the steady-state directly lead to the existence of a short-run positive correlation between money and output and to the appearance of a permanent increase in the price level. More specifically, since the increase in g_t is temporary, there are no changes in the steady-state values; however, this temporary increment in γ_t = (1 − s_t + ρ_tg_t) causes temporary increases in inflation, and in real output, capital and consumption. All these variables return to their original steady-state values, including the inflation rate. Thus the temporary increase in inflation is accompanied by a permanent increase in the price level as predicted by the quantitative theory of money, as well as by short-run real effects. The formal reasonings are those explained in Gutiérrez (2006) for a simpler model.